Disclosure: I’m always looking for things I think my readers will value. This article contains some affilate links to products that I have used and found helpful. If you purchase these, then I may see a share of the revenue. This comes at no extra cost to you.

What is Bubble Sort?

Bubble Sort is a straighthood, easy to understand sorting algorithm. It works by looping through an array and comparing neighbouring elements, then swapping them if they are in the wrong order. In this fashion, the largest number “bubbles” to the top. This is repeated until the array is sorted.

Bubble Sort takes an array, puts it in order, and spits it out:

Bubble Sort is a stable, in-place, and comparison-type algorithm.

Stable means that two elements with equal values will appear in the same order in the sorted output as they appear in the unsorted input array.

For example, if we wanted to sort:

[“Cherries“, “Blackberries”, “Apples”, “Bananas”]

into alphabetical order by first letter, the output would be:

[“Apples”, “Blackberries”, “Bananas”, “Cherries”]

As you can see, “Blackberries” and “Bananas” remained in the same relative positions in the input and output array because the algorithm is stable. Bubble Sort, Merge Sort, and Radix Sort are also stable sorting algorithms.

If the algorithm was unstable, then “Bananas” and “Blackberries” may be interchanged. Selection Sort, Heap Sort and Quick Sort are examples of unstable sorting algorithms.

For a good and simple example of when it’s important to know whether an algorithm is stable or not, check out this article: Important Algorithm Concepts | Algorithm Stability, In-place Algorithms, and Comparison Algorithms

What’s an in-place algorithm? Here’s Wikipedia’s answer: “an algorithm which transforms input using no auxiliary data structure. However, a small amount of extra storage space is allowed for auxiliary variables.”

In simple terms, it usually just means that the input is overwritten (via swapping or replacement) by the output as the algorithm executes. The advantage of in-place algorithms is that they take up less space in memory.

And finally, a comparison sort is a sorting algorithm that only reads the list of elements through a single abstract comparison operation (usually a “less than” or “equal to”) that determines which of the two elements should occur first in the final sorted output array.

Bubble Sort logic

1. Start at the beginning of the array.
2. Is the adjacent element to the right less? If so, swap.
3. Move up to next element.
4. Repeat steps 2-3 until array is sorted.

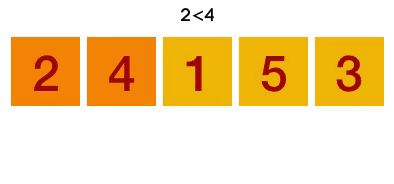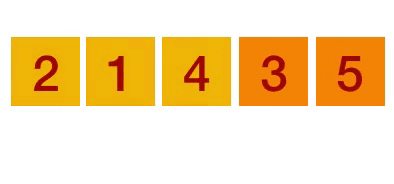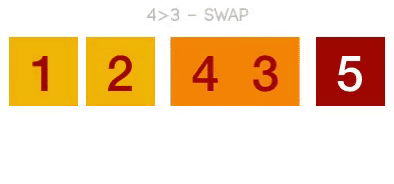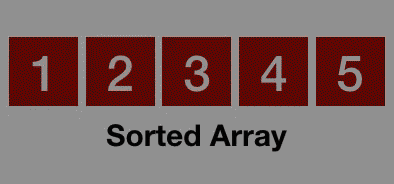
Example: Bubble Sort [3, 2, 4, 1]

First Pass:

1. [3, 2, 4, 1] => is 3 > 2 => yes, so swap: [2, 3, 4, 1]
2. [2, 3, 4, 1] => is 3 > 4 => no, don’t swap
3. [2, 3, 4, 1] => is 4 > 1 => yes, swap: [2, 3, 1, 4]

Second Pass:

4. [2, 3, 1, 4] => is 2 > 3 => no, don’t swap
5. [2, 3, 1, 4] => is 3 > 1 => yes, swap: [2, 1, 3, 4]
6. [2, 1, 3, 4] => we already know 4 is the biggest as it bubbled to the top in the first pass.

Third Pass

7. [2, 1, 3, 4] => is 2 > 1 => yes, so swap: [1, 2, 3, 4]
8. Sorted!

Implementing Bubble Sort in JavaScript

Here is a simple, unoptimized solution to Bubble Sort:

function bubbleSort(arr) {
  for (let i = arr.length - 1; i > 0; i--) {
    for (let j = 0; j < i; j++) {
      if (arr[j] > arr[j + 1]) {
        // SWAP
        ;[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
      }
    }
  }
  return arr
}
console.log(bubbleSort([2, 3, 1, 2])) // [1, 2, 2, 3]

How this works:

1. Start looping with a variable called i from the end of the array toward the beginning
2. Start an inner loop with a variable called j from the beginning until i – 1
3. If arr[j] is greater than arr[j+ 1], swap those two values
4. Return the sorted array

The problem with the above solution is that it is very inefficient if the data is almost sorted to begin with; it will keep on iterating through even if no swaps were made.

Here’s a more optimized Bubble Sort:

function bubbleSort(arr) {
  let noSwaps
  for (let i = arr.length - 1; i > 0; i--) {
    noSwaps = true
    for (let j = 0; j < i; j++) {
      if (arr[j] > arr[j + 1]) {
        // SWAP
        ;[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
        noSwaps = false
      }
    }
    if (noSwaps) break
  }
  return arr
}
console.log(bubbleSort([2, 3, 1, 2])) // [1, 2, 2, 3]

In the above solution, if there are no swaps during the inner loop, then it means that the array is sorted and we can break out of the outer loop; the sorted array is then returned.

As you can see, we had to store an extra variable in memory, noSwaps, in order to improve the execution time of the algorithm. This is often the case with algorithms: there is a trade-off between space and time.

Bubble Sort performance

We’ll now discuss the performance of Bubble Sort in terms of Big O Notation.

Best case complexity of Bubble Sort

The best case complexity of Bubble Sort occurs when the array is nearly sorted and only requires one run-through with swaps. The next pass through involves no swaps, so we break out of the loop after a total of two iterations.

Therefore, our best case is of O(2n), where n is the length of the input array. This can be simplified to O(n) => linear runtime at best case.

Worst case complexity of Bubble Sort

The worst case complexity of Bubble Sort occurs if the array is “very” unsorted - e.g. in reverse.

There are n elements in the array. For each of these elements, we make n comparisons. That’s n * n = n^2 operations, so the Big O of Bubble Sort is O(n^2) – quadratic time complexity.

Average case complexity of Bubble Sort

In average case – if the elements are "randomly distributed" – Bubble Sort may require n/2 passes and O(n) comparisons for each pass. Therefore, the average case time complexity of Bubble Sort is O((n / 2) * n) = O(n^2 / 2). This simplifies to O(n^2)

Bubble Sort space complexity

The space complexity of Bubble Sort is O(1) – constant space. This is because there are only two additional memory spaces required: the two loop iterator variables, i and j. No matter the length of the input array, there will only ever be two variables needed to be stored in memory (unless we are using the noSwaps optimisation variable, then there will be three variables in memory).

Bubble Sort Performance summary table

When to use Bubble Sort

Bubble Sort has the advantage of being a very easy to understand algorithm; however, Bubble Sort is usually not a good choice due to its quadratic time complexity.

This can be improved upon: Merge Sort, for example, runs at O(n log(n)) on average and at worst case, but also runs at O(n log(n)) at best – worse than Bubble Sort if the array is almost sorted.

So, Bubble Sort is only really a viable option if the array is almost sorted, or if the input array is small enough for you to not have to worry about performance.

Overall, you probably won't be implementing many Bubble Sorts in your lifetime! Insertion Sort is often a better choice for small arrays, or arrays that are almost sorted. And Merge Sort or Quick Sort are better options for larger arrays.

If you enjoyed this post, subscribe to my newsletter. I write on topics such as algorithms, UI design and freelancing. I’ll email you once per week with my latest article and bonus tips and tricks. I like to dive deeply into topics to give you all the information you need in one place!

And if you want to further your knowledge of algorithms and data structures, check out: JavaScript Algorithms and Data Structures Masterclass by Colt Steele. It’s the best Udemy course I’ve ever taken 👌.

Thanks for reading,

Have a great day!